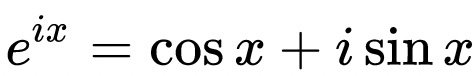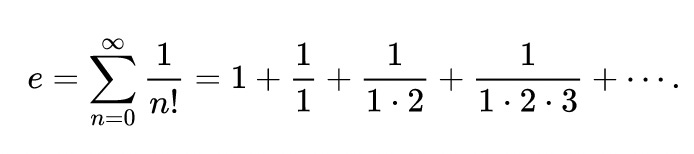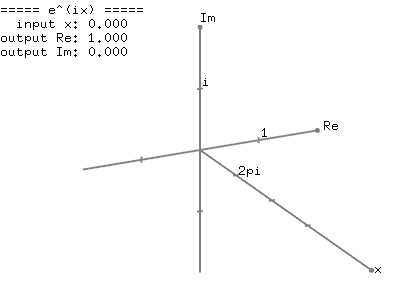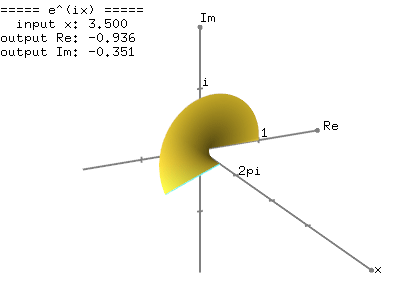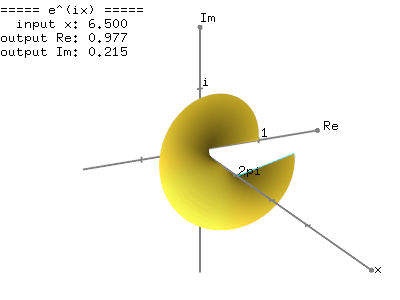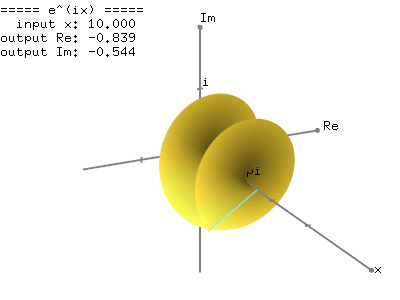Euler's formula as a model for the universe
Euler’s formula relates imaginary numbers, the natural logarithm, trigonometry, and the ratio of a circle’s diameter and circumference, all in a single equation. I would like to propose that this equation can also describe the potential and kinetic energy of an ideal oscillating system, and, in doing so, provide a useful model for the hypothetical expansion and contraction of the universe.
The equation is written as follows:
If math isn’t your thing, I’ll explain the symbols real quick…
e, also known as Euler’s number, is the base of the natural logarithm. Like pi, e is an irrational number with decimal places that continue endlessly. Its first digits are 2.718, and it’s defined by the following series:
Perhaps the easiest way to think of e is in terms of compound interest…
If I give you a dollar and say that I will pay you 100% interest per year, you would expect to have $2 at the end of the year, presuming that I compute and credit the interest just one time, at the end of the year.
If the interest is credited twice in the year, the interest rate for each 6 months would be 50%… So after 6 months, I’d give you fifty cents, and you’d have $1.50. Then, at the end of the year, I’d be paying you 50% interest on the new sum of 1.50, so you’d get another 75 cents and end up with $2.25 total.
If we keep on increasing the number of intervals, the same rules apply. Quarterly payments would give you $2.44 at the end of the year, monthly payments would give you $2.61, and if we increase the number of intervals towards infinity, so that I’m paying you interest almost constantly, tiny payments every second of every day, the money I owe you doesn’t go toward infinity, it goes toward e:
$2.718281828…
There’s plenty more we could say about e and its properties, but you get the general picture.
The next symbol that might need some explanation is i.
i is the square root of -1.
i x i = -1
We don’t usually think of negative numbers as having square roots, but using imaginary numbers allows us to imagine that they do. If we imagine the real number line as an axis running from negative infinity, past zero, and to positive infinity, we can imagine the imaginary axis as another axis perpendicular to this x-axis. Complex numbers, which have a real component and an imaginary component, are plotted just like they would be on an (x,y) coordinate plane, except that the “y” in this case is the imaginary axis instead of a real axis.
Kinetic and Potential Energy
Kinetic energy (KE) is the energy of an object by virtue of its motion. In classical mechanics, it’s defined as e = (1/2)mv².
Potential energy (PE) is the energy of an object by virtue of its position (other factors as well, but let’s just focus on position). The PE equation must be adjusted depending on the system and the nature of the potential energy. With a falling object, it can be defined as PE = mgh, where g is gravitational acceleration and h is the height of the object. For a compressed or stretched spring, we have PE = (1/2)kx2, where k is a constant which represents the stiffness or force of the spring and x is the displacement from the equilibrium point.
These mathematical definitions of KE and PE are useful within the context of arbitrarily-defined mechanical systems, but they are not universally applicable. For our purposes, we need only understand KE and PE as abstract concepts.
The important ideas to take away:
KE is the energy of an object’s motion
PE is the energy of an object’s position (or potential for creating motion)
All energy values are defined by the units: e = mass * velocity²
The sum energy of KE + PE in any system is conserved
Potential energy, as it’s expended, transforms itself into kinetic energy. Kinetic energy, like that of a pendulum swinging past its equilibrium point and being slowed down by gravity, transforms itself into potential energy. This is what we mean by the conservation of energy: it never vanishes, just changes form.
In a normal system, defined by our own arbitrary limits, energy is inevitably lost. It escapes from the system through surface friction, air resistance, heat loss, and a thousand different factors we can’t always account for, so that the total energy of our system is always decreasing.
But what if we imagine an ideal oscillating system, one that is so efficient, or so all-encompassing, that no energy can ever escape it? How would we graphically represent its balance of energy?
Euler’s formula provides a novel and profound solution.
Graphing Energy Using Euler’s Formula
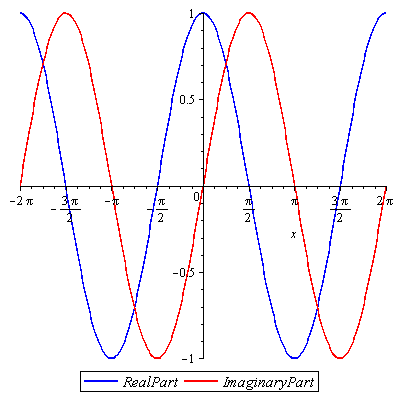
If you enter Euler’s formula into Wolfram Alpha, or another graph generator, you’re likely to end up with a graph that looks like this…
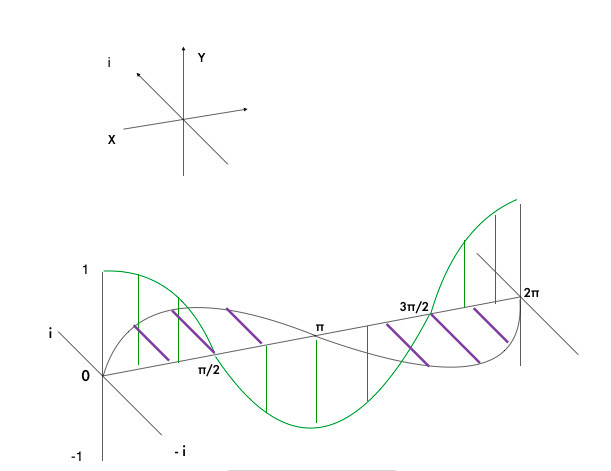
…where the cosine (blue/real) and sine (red/imaginary) values are superimposed on the same x-y plane. While this is perhaps a convenient way to draw the graph, it’s not entirely accurate. When we multiply something by i, the imaginary unit, we are in essence rotating that value by 90 degrees from the real axis into the imaginary axis. A better way to draw the graph would be to show this third axis, the imaginary dimension, and draw the sine wave there, perpendicular to the cosine wave.
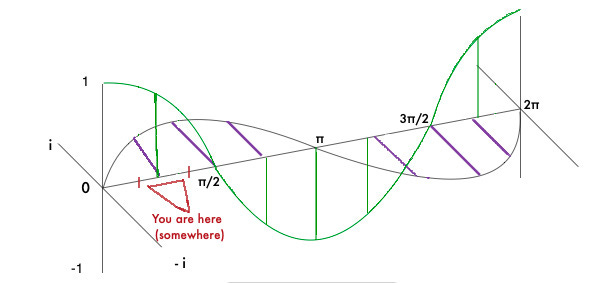
Please forgive my hideous, microsoft-paint rendition of the graph. I never claimed to be a graphic design expert. Hopefully the three-dimensionality and helix structure of the graph is self-evident.
The green wave is our cosine x, existing in the real (x,y) plane. The purple wave is our i*sine x, existing in the imaginary (x,z) plane.
The relationship to an oscillating system is quite simple. Let Cos(x) represent potential energy. Let i*Sin(x) represent kinetic energy. Let x represent time.
If we compress a perfect spring, in the moment that we release it (x= 0) it would have maximum potential energy and no kinetic energy. That potential energy begins to rapidly accelerate the spring and convert itself into kinetic energy, which reaches a maximum at the equilibrium point (x = π/2) just as the PE reaches 0. Momentum carries the spring onwards, past the equilibrium point, and now an opposite form of tension is developing in the spring, a negative force which will sap the KE and reach its maximum just as the tip of the spring stops moving forward (x = π). The negative PE snaps the spring back toward center, repeating the same process in reverse, accelerating the spring until the moment of the equilibrium point (x = 3π/2), where the direction of the force reverses again, slowing the spring down and the diminishing the KE until it stops moving at its most compressed point, the point where we began… x = 0 or x = 2pi, where the spring will shoot out again and the cycle will repeat. In an ideal oscillating system, there’s no substantial difference between these “beginning” and “ending” moments.
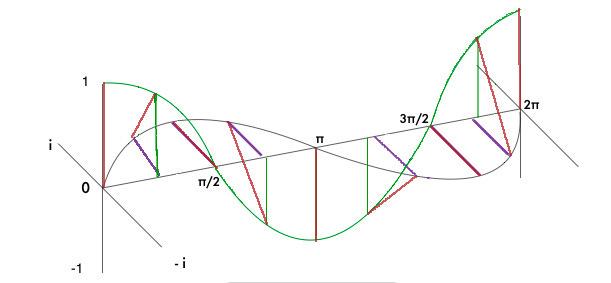
An astute reader may have already considered that sin(x) and cos(x) values do not add up to a consistent sum at any given x input. For instance, sin(0) + cos(0) = 1, but Sin(π/4) + cos(π/4)= 1.414. The sum of KE and PE must be consistent if we are going to accord with the law of conservation of energy, so we would seem to have a big problem, but this problem only results from erroneously placing both graphs on the same axis. It disappears when we consider i*sin(x) as existing on the imaginary plane. Instead of the basic addition of sin(x) + cos(x), we must perform a vector addition, essentially measuring the distance between the two waves at any given x value.
The red lines represent our vector addition. Regardless of the direction of the line, it has an absolute magnitude of 1, because the sum calculation is equivalent to finding the hypotenuse “a” with the Pythagorean theorem, a² = b² + c² . At any given x, the sum of the squares of sine or cosine will always equal one, and so, for the purpose of our metaphor, energy is conserved.
This method of summarizing the energy is interesting because, while maintaining a consistent and unchangeable magnitude, it also describes the shifting character of that total energy, in terms of its balance between kinetic and potential energy. In the gif below, we can imagine the length of the green bar as the total energy at any given moment and the direction of the green bar as the character of that energy at any given moment.
The Universe as an Ideal Oscilating System
We do not know if the universe is infinite or finite. We do not know the shape of the universe or how many dimensions it has. On a macro scale, the only thing we know with certainty is that the galaxies we see in our telescopes are moving away from each other, and the speed at which they are moving away from each other is increasing.
Now we enter the realm of pure hypothesis and thought experiment. We will have to make some broad assumptions and see what they lead to.
From the observation that galaxies are accelerating away from each other, physicists have come to a general consensus that the universe is expanding and, by the same token, that matter in the universe was at one time much closer together, collated in an area of extreme density—a singularity—and this infinitely dense point exploded outwards in a “Big Bang” to form the present state of the visible universe.
While we cannot say with certainty that all the energy in the universe was once condensed at a single point, we can logically presume from observation that the visible matter was once far more condensed than it is now. We can use the Big Bang as an ideal limit, reality taken to a logical extreme. History may not have played out in exactly that way, but we can be sure that history played out within the confines of that logical limit.
In an ideal oscillating system, the moment of the big bang is logically equivalent to our maximally compressed spring or our pendulum held aloft. At this hypothetical moment of singularity, the kinetic energy of the universe would be zero, because absolutely nothing is in motion. There is a maximum amount of potential energy, an unimaginably high outward pressure resulting from the superposition of all visible matter. Instantaneously, this pressure must explode the condensed matter outward, and in doing so transform itself into kinetic energy. The expansion of the system continuously accelerates so long as there remains positive potential energy to exert outward force.
At this point, we have to ask some fundamental questions about the nature of matter, mass, gravity, energy, and space. When we talk about matter being compressed into a single point, what about space? Does the universe still exist outside that point, like an infinite sea of empty space? Or is space itself compressed into the singularity as well? Is the outward expansion of disparate galaxies also the outward expansion of space itself? And what do we mean by an “outward force?” What’s the source of this force? What’s pushing everything away?
According to most physicists, the outward force behind the accelerating expansion of the universe comes from “dark matter,” so-named because we can’t see it, but it appears to account for up to 85% of the total mass in the universe.
Positing an entirely new form of matter seems like an unnecessary complication to a simple problem. We have known since the dawn of Einstein’s General Relativity that space itself is embued with physical properties and is the mediator of gravity. If we accept that the field of space-time is responsible for the attraction between disparate objects, we should not be surprised that it is also responsible for their repulsion. The subjective appearance of “missing mass” disappears if one considers the possiblity that mass is a function of the distortion of space. Rather than merely affecting the curvature of space-time, as is proposed in General Relativity, mass may be better defined as the curvature itself.
I’m getting ahead of myself though. Re-defining mass warrants a much lengthier defense and discussion. In one of my next articles, I will get into the meat of this new definition of mass, the reasons it is viable, and the plethora of implications it could have for our understanding of the universe.
For now, whether we refer to the unseen pressure as a consequence of "dark matter" or of space itself, we only know two things:
It accounts for roughly 85% of mass in the universe.
Energy must be expended in order to generate the outward force.
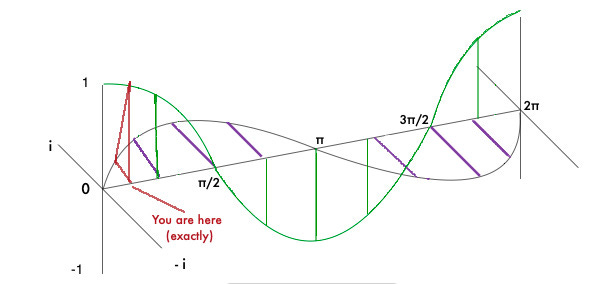
Knowing #1, and applying it to our graph of Euler’s formula, we could potentially make a rough approximation our position in the history of time. If the 85% directly corresponded to the PE, it would be as easy as saying: “we are at the position of 85% PE and 15% KE,” then with some simple mathematics, square root of .85, square root of .15, we could determine that we are at the point of .921 + .387i, or roughly π/8 on the x axis.
Of course, it is not quite so simple. We cannot presume that dark energy is an exact 1/1 corrollary to PE, and we also cannot presume that this 85% estimation is particularly accurate, even less so when we are going to adjust our definition of what mass really is. In any case, it’s enticing to think that with Euler’s formula we could have a model to predict the future in a very rough way. By estimating our position x, we could estimate the amount of time until the “equilibrium point” at π/2, the “Big Crunch” at π, or the next “Big Bang” at 2π. It is also enticing to think of time as a circle, space as a form of energy… Reality itself can compress, expand, and stretch past its equilibrium point, just like a spring.